实验原理

1.迈克尔逊干涉仪

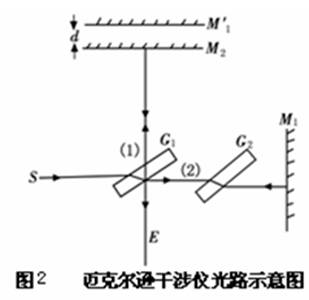
图1是迈克尔逊干涉仪实物图。图2是迈克尔逊干涉仪的光路示意图，图中Ｍ₁和Ｍ_２是在相互垂直的两臂上放置的两个平面反射镜，其中Ｍ₁是固定的；Ｍ_２由精密丝杆控制，可沿臂轴前、后移动，移动的距离由刻度转盘(由粗读和细读2组刻度盘组合而成)读出。在两臂轴线相交处，有一与两轴成45°角的平行平面玻璃板G₁，它的第二个平面上镀有半透（半反射）的银膜，以便将入射光分成振幅接近相等的反射光⑴和透射光⑵，故G₁又称为分光板。G₂也是平行平面玻璃板，与G₁平行放置，厚度和折射率均与G₁相同。由于它补偿了光线⑴和⑵因穿越G₁次数不同而产生的光程差，故称为补偿板。从扩展光源S射来的光在G₁处分成两部分，反射光⑴经G₁反射后向着Ｍ_２前进，透射光⑵透过G₁向着Ｍ₁前进，这两束光分别在Ｍ_２、Ｍ₁上反射后逆着各自的入射方向返回，最后都达到E处。因为这两束光是相干光，因而在E处的观察者就能够看到干涉条纹。

由M１反射回来的光波在分光板G₁的第二面上反射时，如同平面镜反射一样，使Ｍ₁在Ｍ_２附近形成Ｍ₁的虚像Ｍ₁′，因而光在迈克尔逊干涉仪中自Ｍ_２和Ｍ₁的反射相当于自Ｍ_２和Ｍ₁′的反射。由此可见，在迈克尔逊干涉仪中所产生的干涉与空气薄膜所产生的干涉是等效的。当Ｍ_２和M１′平行时(此时M１和Ｍ_２严格互相垂直)，将观察到环形的等倾干涉条纹。一般情况下，Ｍ₁和Ｍ_２形成一空气劈尖，因此将观察到近似平行的干涉条纹(等厚干涉条纹)。

2.单色光波长的测定

用波长为λ的单色光照明时，迈克尔逊干涉仪所产生的环形等倾干涉圆条纹的位置取决于相干光束间的光程差，而由Ｍ_２和Ｍ₁反射的两列相干光波的光程差为

Δ＝2dcosi (1)

其中i为反射光⑴在平面镜Ｍ２上的入射角。对于第k条纹，则有

2dcosi_k＝kλ (2)

当Ｍ２和Ｍ₁′的间距d逐渐增大时，对任一级干涉条纹，例如k级，必定是以减少cosi_k的值来满足式(2)的，故该干涉条纹间距向i_k变大(cos i_k值变小)的方向移动，即向外扩展。这时，观察者将看到条纹好像从中心向外“涌出”，且每当间距d增加λ/2时，就有一个条纹涌出。反之，当间距由大逐渐变小时，最靠近中心的条纹将一个一个地“陷入”中心，且每陷入一个条纹，间距的改变亦为λ/2。因此，当Ｍ２镜移动时，若有N个条纹陷入中心，则表明Ｍ_２相对于Ｍ₁移近了

（3）

反之，若有N个条纹从中心涌出来时，则表明Ｍ_２相对于Ｍ₁移远了同样的距离。

如果精确地测出Ｍ_２移动的距离Δd，则可由式(3)计算出入射光波的波长。

3.点光源的非定域干涉现象

由于光源性质的不同，用迈克尔逊干涉仪可观察定域干涉和非定域干涉。用Ｈｅ-Ｎｅ激光做光源，使激光束通过扩束镜会聚后发散，此时就得到了一个相干性很好的点光源。它发出的球面波先被分光板Ｐ_１分光，然后射向两全反射镜，经Ｍ_１和Ｍ_２反射后，在人眼观察方向就得到了两个相干的球面波，它们如同是由位于Ｍ_１后的两个虚点光源Ｓ_１和Ｓ_２产生的，如图3所示。由两虚点光源产生的两列球面波，在空间相遇处都能进行干涉，干涉条纹不定域，故称非定干涉。非定干涉的图样，随观察屏的不同方向和位置而不同。当观察屏垂直于Ｓ_１和Ｓ_２连线时,是同心圆条纹，圆心是Ｓ_１和Ｓ_２连线延长线和屏的交点。如转动观察屏不同角度，则可看到椭圆，双曲线和直线等几种干涉图样。

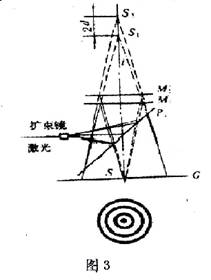
如调节反射镜Ｍ_２的微调螺钉，使Ｍ_１‖Ｍ_２＇，此时和Ｍ_１平行放置的观察屏上就出现同心圆条纹，圆心在光场中心。两虚点光源的间距为Ｍ_１和Ｍ_２间距ｄ的两倍，即圆心处光程差为2ｄ。与前面讨论等倾干涉情况类似，当ｄ增加时，中心条纹一个个“冒出”，反之，一个个“缩进”。这时同样也可用公式(3)来计算波长。

4.定域干涉现象

（１）当使用扩展的面光源时，只能获得定域干涉。定域干涉因形成的干涉条纹有一定的位置而得名。定域干涉又分为等倾干涉和等厚干涉，这取决于Ｍ_１和Ｍ_２是否垂直，或者说Ｍ_１和Ｍ_２′是否平行。Ｍ_２′是反射镜Ｍ_２被分光板Ｐ_１反射所成的虚像。

　　①等倾干涉

当Ｍ_１和Ｍ_２′互相平行时，得到的是相当于平行平面板的等倾干涉条纹，其干涉图样定位于无限远，如果在Ｅ处放一会聚透镜，并在其焦平面上放一屏，则在屏上可观察到一圈圈的同心圆。对于入射角ｉ相同的各束光，如下图所示，其光程差均为：

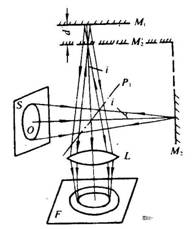
　　　　　　δ＝2ｄCOSｉ　　　　　（4）

　　对于ｋ级亮条纹，显然是由满足下式的入射光反射而成的：

　　　　　　δ＝2ｄCOSｉ＝ｋλ　　（5）

　　在同心圆的圆心处ｉ＝０，干涉条纹的级数最高，此时有：

　　 δ＝2ｄ＝ｋλ　　　　　（6）

　　当移动Ｍ_１使间隔ｄ增加时，圆心的干涉级次增加，我们就可看到中心条纹一个一个向外“冒出”，而当ｄ减小时，中心条纹将一个一个地“缩”进去。每“冒出”或“缩进”一个条纹，ｄ就增加或减小了λ／2。如果测出Ｍ_１移动的距离Δｄ，数出相应的“冒出”或“缩进”的条纹个数Δｋ，就可以算出光源的波长：

　　　　　　λ＝2Δｄ／Δｋ

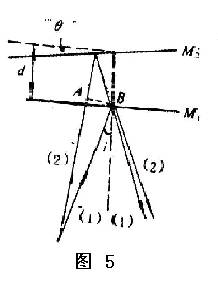
②等厚干涉

当Ｍ_１和Ｍ_２′不平行而有一个很小的角度时，形成一个楔形的空气层，这时就将出现等厚干涉条纹,如下图所示。当ｄ很小,即Ｍ_１和Ｍ_２′相交时，由面光源上发出的光束，经楔形空气薄层两面反射所产生的等厚干涉条纹定位于楔形空气层的表面。要看清楚这些条纹，眼睛必须聚焦在Ｍ_１镜附近，也可用凸透镜将空气楔成象在其共轭面上。此时，相干处的光程差公式仍如上面的（１）式，由于ｄ很小，光程差的变化主要取决于ｄ的变化，入射角变化的影响可以忽略不计。因此在空气楔上厚度相同的地方有相同的光程差，我们就可以观察到平行于楔棱的直条纹。当ｄ增大时，入射角ｉ的变化对光程差的影响不能忽略，此时将引起条纹的弯曲，并凸向楔棱一边，即凸向Ｍ_１和Ｍ_２′的交线。