实验原理

光波在介质中传播时被超声波衍射的现象，称为超声致光衍射（亦称声光效应）。

超声波作为一种纵波在液体中传播时，超声波的声压使液体分子产生周期性的变化，促使液体的折射率也相应的作周期性的变化，形成疏密波。此时，如有平行单色光沿垂直于超声波传播方向通过这疏密相同的液体时，就会被衍射，这一作用，类似光栅，所以称为超声光栅。

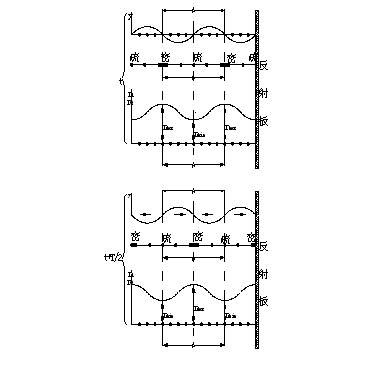
超声波传播时，如前进波被一个平面反射，会反向传播。在一定条件下前进波与反射波叠加而形成超声频率的纵向振动驻波。由于驻波的振幅可以达到单一行波的两倍，加剧了波源和反射面之间液体的疏密变化程度。某时刻，纵驻波的任一波节两边的质点都涌向这个节点，使该节点附近成为质点密集区，而相邻的波节处为质点稀疏处；半个周期后，这个节点附近的质点有向两边散开变为稀疏区，相邻波节处变为密集区。在这些驻波中，稀疏作用使液体折射率减小，而压缩作用使液体折射率增大。在距离等于波长A的两点，液体的密度相同，折射率也相等，如图一所示。

单色平行光λ沿着垂直于超声波传播方向通过上述液体时，因折射率的周期变化使光波的波阵面产生了相应的位相差，经透镜聚焦出现衍射条纹。这种现象与平行光通过透射光栅的情形相似。因为超声波的波长很短，只要盛装液体的液体槽的宽度能够维持平面波（宽度为ι），槽中的液体就相当于一个衍射光栅。图中行波的波长A相当于光栅常数。由超声波在液体中产生的光栅作用称作超声光栅。

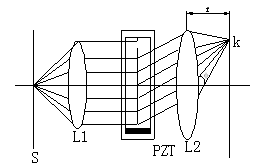
图二 WSG-I超声光栅仪衍射光路图

液体疏密分布和折射率n的变化

图一 在t和t+T/2 (T为超声振动周期)两时刻振幅y

当满足声光喇曼－奈斯衍射条件：2πλι/A²<<1时，这种衍射相似于平面光栅衍射，可得如下光栅方程（式中k为衍射级次，φ_k为零级与k级间夹角）

在调好的分光计上，由单色光源和平行光管中的会聚透镜（L₁）与可调狭缝S组成平行光系统，如图二所示。

让光束垂直通过装有锆钛酸铅陶瓷片（或称PZT 晶片）的液槽，在玻璃槽的另一侧，用自准直望远镜中的物镜（L₂）和测微目镜组成测微望远系统。若振荡器使PZT晶片发生超声振动，形成稳定的驻波，从测微目镜即可观察到衍射光谱。从图二中可以看出，当φ_k很小时，有：

其中l_k为衍射光谱零级至k级的距离；f为透镜的焦距。所以超声波波长：

超声波在液体中的传播的速度：

式中的v是振荡器和锆钛酸铅陶瓷片的共振频率，Δl_k为同一色光衍射条纹间距。